Blender 3d : Cathédrale de Reims – 1

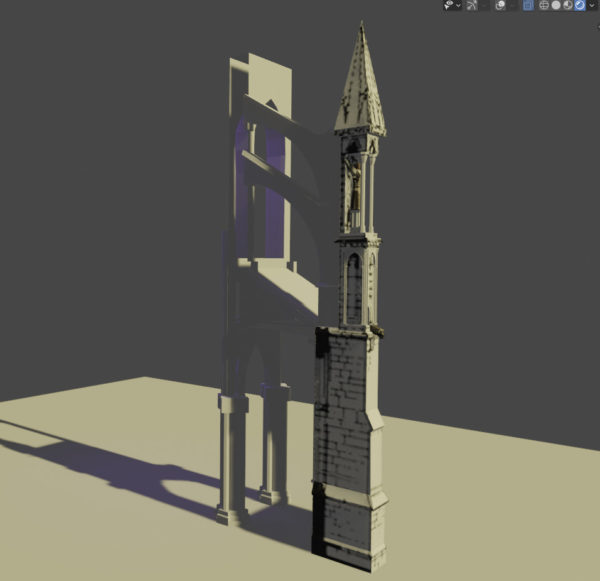
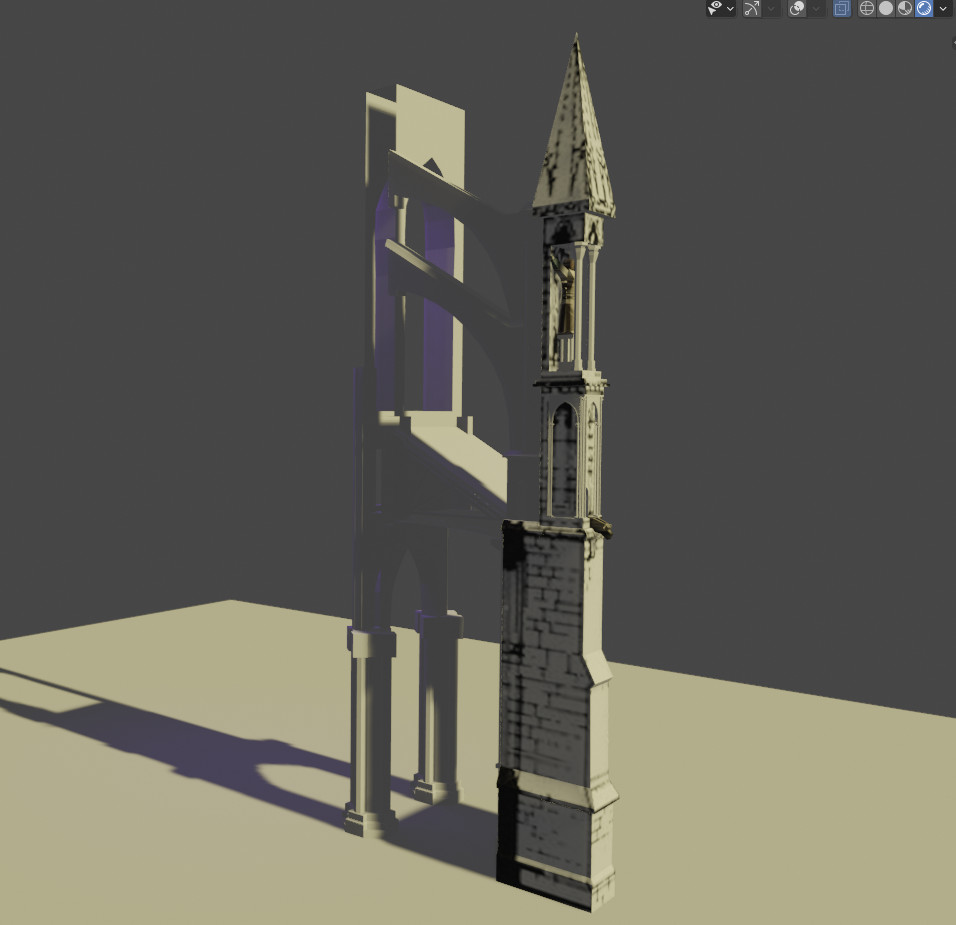
J’apprends à utiliser le logiciel Blender depuis quelques mois et il est temps de passer à une belle problématique : la gestion d’un ensemble complexe d’objets… Voilà donc le projet Cathédrale ! Cet article sera (un peu) long et mêlera une grosse partie d’histoire et un peu de technique.

I/ Le commencement

J’ai décidé de créer 2 chapitres : le chapitre suivant intéressera ceux qui veulent apprendre à modéliser sous Blender (ou qui sont curieux de voir comment faire) mais si vous êtes intéressé seulement par les cathédrales vous pouvez passer directement au chapitre III !

II/ La construction sous Blender

Si comme moi vous avez suivi de nombreux tutos, que vous connaissez le texturing basique (création de textures persos, UV, etc) et que vous connaissez les bases de la modélisation polygonale.. En gros si vous arrivez à modéliser des objets simples assez rapidement et que vous n’hésitez pas à détruire sans pitié une partie du maillage pour le recréer autrement : vous êtes prêts pour la suite!
Je veux que la cathédrale soit la plus précise, ou plus exactement la plus réaliste possible. Le premier objectif a donc été de trouver des plans avec des dimensions et de fouiller le web à la recherche d’informations et également d’avoir quelques photos pour comparer les résultats. Une fois ces images poche il va falloir les importer et adapter leurs tailles dans Blender. Grossièrement il va falloir les convertir des pixels en mètres!

1/ l’importation des images

Vous avez 2 méthodes :
– le glisser/déposer de l’image dans la fenêtre de Blender qui créera un objet image (l’avantage c’est que l’image sera toujours visible même en mode wireframe).
– l’import via le plugin ‘Import Image as Plane‘ qui créé un objet avec un maillage de type plan avec une texture image (option que je préfère car plus flexible).

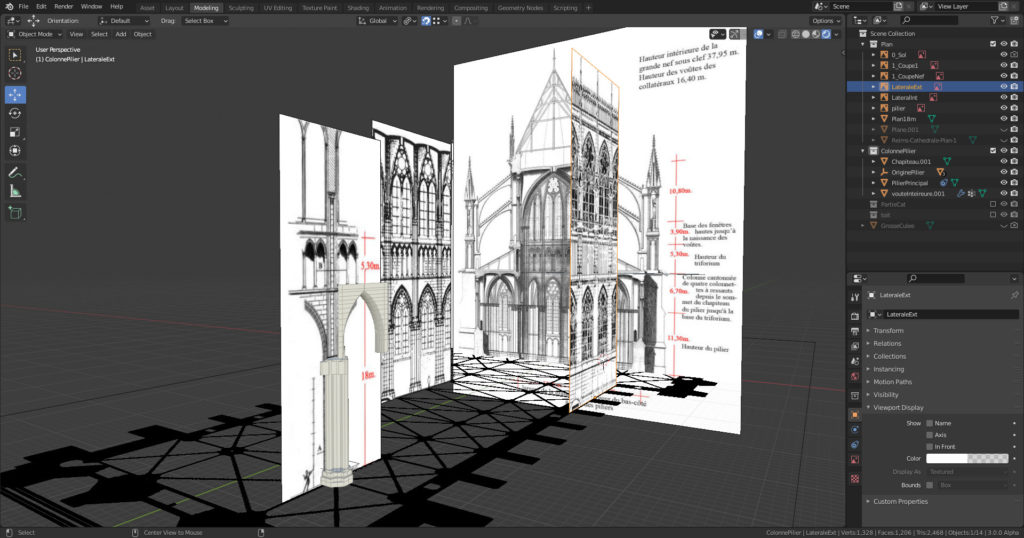
2/ Origine et mise à l’échelle

Pour harmoniser la taille des images et qu’elles représentent toutes les bonnes dimensions sur Blender l’astuce est de définir leur origine en Z=0 au niveau du sol et au centre de symétrie de la cathédrale.

Pour l’agrandir à la bonne échelle il suffit alors de créer un plan à la distance repérée et d’agrandir proportionnellement l’image ([S] + souris) jusqu’à ce que le repère de l’image se confonde avec le plan : simple mais efficace! Voici la petite capture d’écran :

3/ Découpage et vérifications

Avec l’image importée comme objet plan vous pouvez redécouper les parties inutiles de l’image ( [Ctrl]+[R] pour créer un edgeloop et vous supprimer les faces inutiles).
Pour positionner les images sans côtes les uns par rapport aux autres il va falloir comparer leur hauteur avec des éléments tangibles : position des piliers pour le plan d’élévation, la clé de voute principale, le plan de base du Triforium, etc

4/ Le début de la modélisation

Le problème est de savoir par quoi commencer et cela dépend de ce que vous recherchez! Si votre objectif est purement graphique c’est à dire de modéliser rapidement l’extérieur de la cathédrale il vous suffira de :
1: partir du plan d’élévation (la vue de dessus) et de monter tous les murs avec des extrusions
2: de modéliser la découpe des fenêtres et de l’utiliser comme outil de découpe avec la fonction booléenne de soustraction
3: etc.
En gros il vous suffira de tailler dans la masse en prenant à chaque fois vos images comme repère. La cathédrale pourra donc rapidement être modélisée…

Par contre mon objectif n’est pas seulement de modéliser un bâtiment vite fait, j’ai envie de comprendre les techniques de modélisation d’ensembles complexes et de me rapprocher du processus de construction des bâtisseurs. C’est pourquoi je suis parti sur une approche d’assemblage d’éléments (colonne, chapiteau, etc) un peu comme un bâtisseur mais aussi comme un concepteur (CAO).

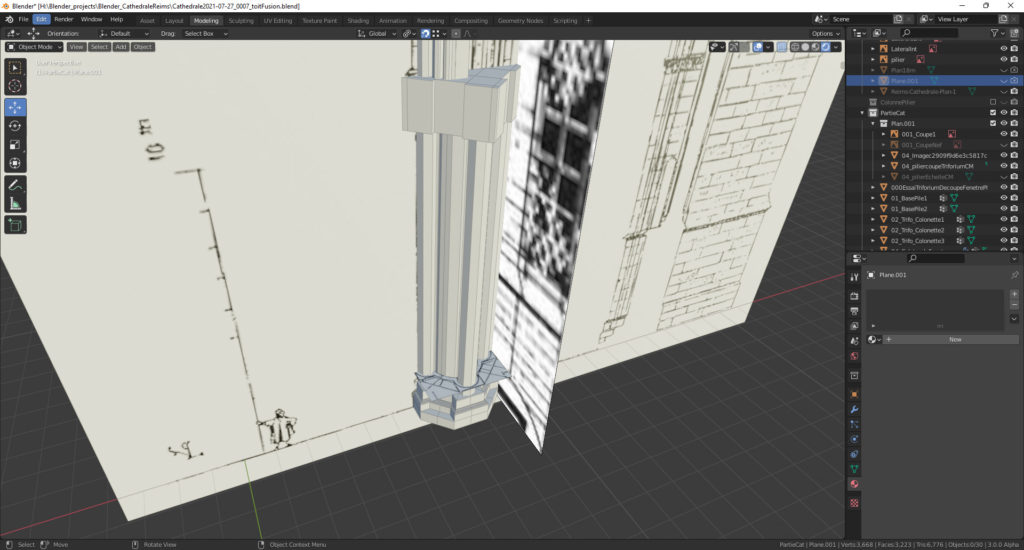
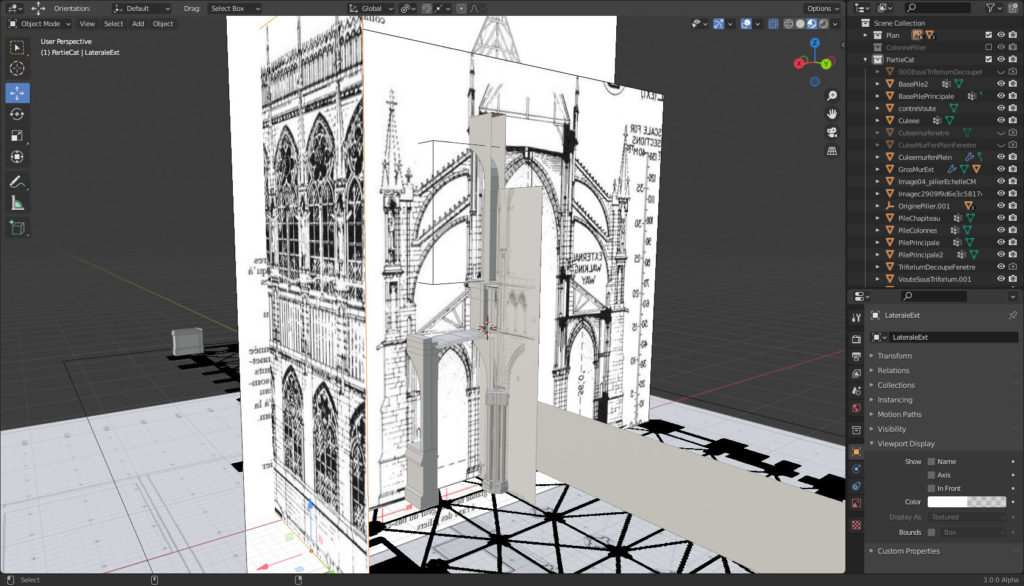
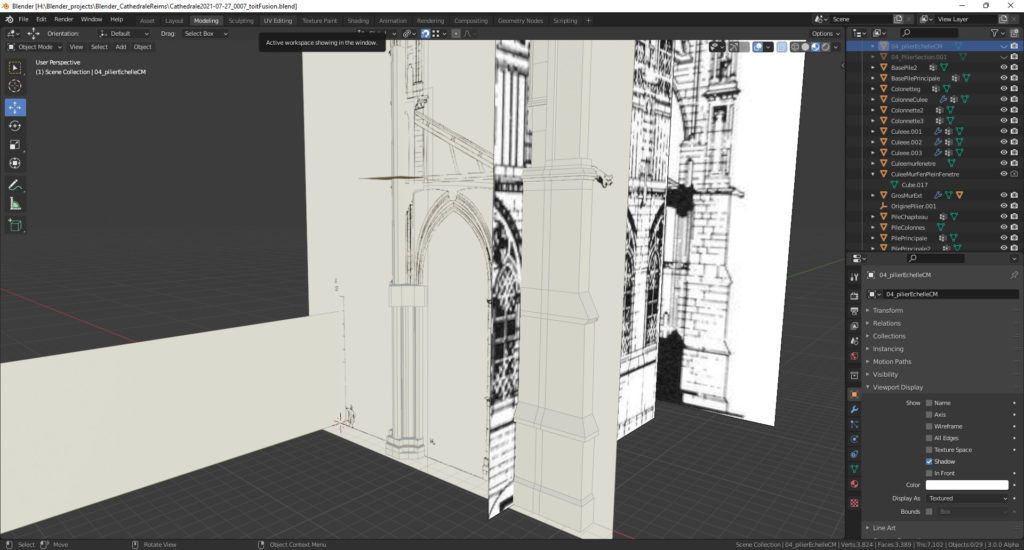
L’avantage de cette méthode c’est que même si le pilier n’est pas à la bonne position je peux facilement le déplacer et je ne suis pas obligé de modéliser chaque élément proprement : je peux commencer par un simple cylindre et le remplacer plus tard par un modèle plus élaboré..

5/ Les vérifications

Par les photos et sans trop non plus tomber dans l’excès (correction de lentille de l’appareil, etc) je peux quand même comparer certaines parties de mes photos avec les plans pour voir si les hauteurs semblent cohérentes :

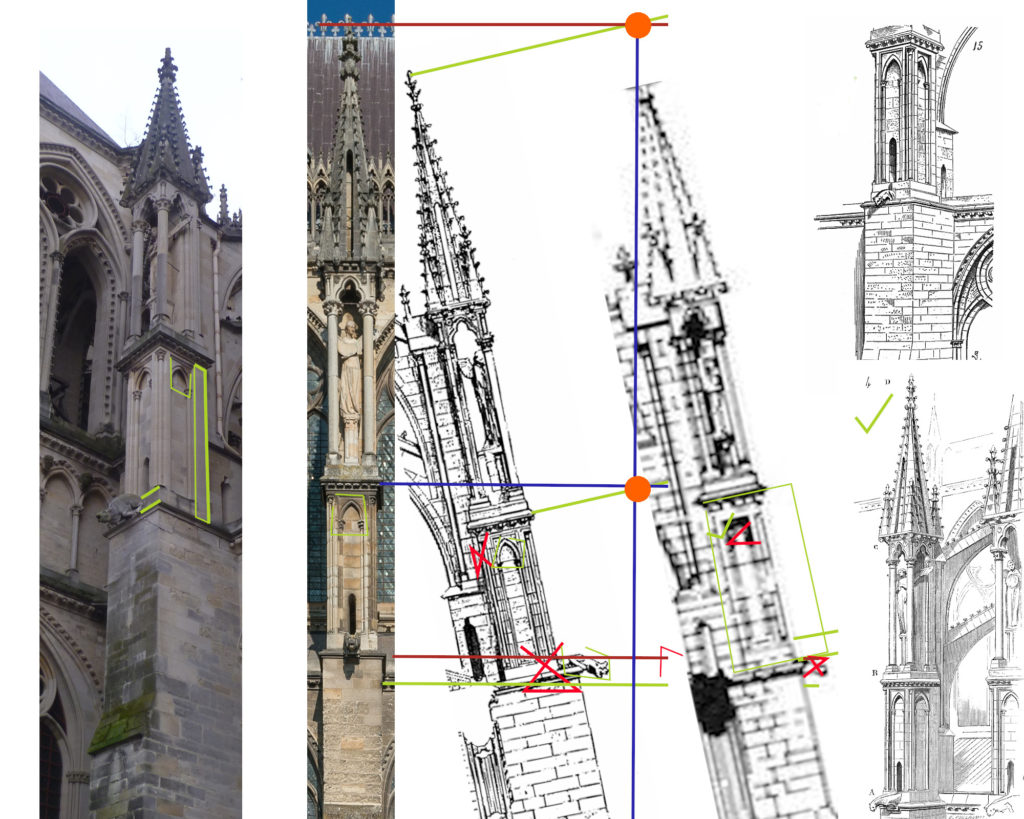
Enfin je peux faire un rendu de la vue de côté du modèle de Blender et la coller sur une vraie photo avec une déformation 3D :

C’est bien de pouvoir vérifier mais ce serait mieux d’avoir un plan précis ou une base de calcul solide et de savoir par quoi commencer…
Si vous êtes curieux de savoir pourquoi je commence par les piliers, si vous êtes intéressés par les mesures, la construction des cathédrales et peut être aussi par les mythes qui entourent ces constructions et les théories quasi divines : la suite est faite aussi pour vous!

III/ La construction d’une cathédrale

Si je veux être précis je vais quand même rapidement être confronté au problème de position car les images agrandies à une telle échelle sont peu précises… En plus quand on commence à s’y intéresser de près on s’aperçoit qu’elles ne sont pas identiques et voilà un petit montage pour vous le montrer :

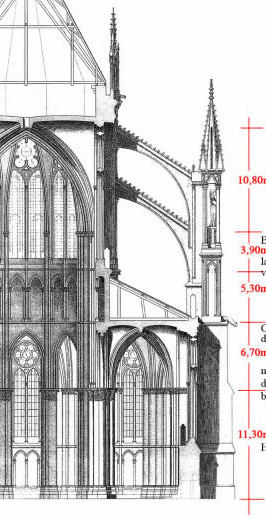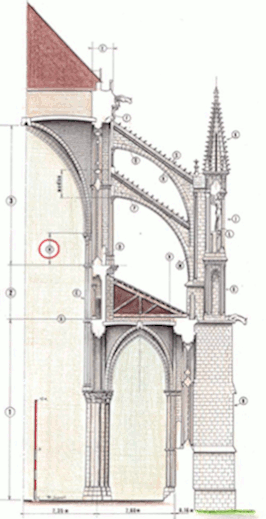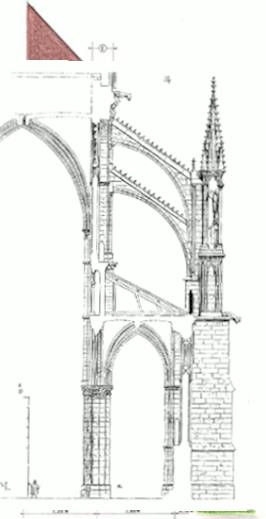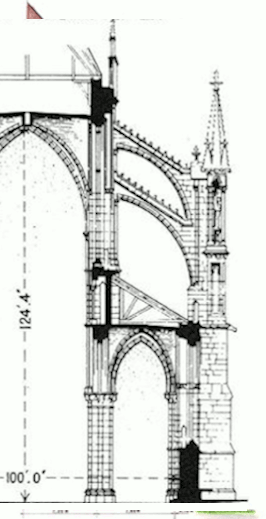
Quelque part cela m’arrange parce que c’est un beau prétexte pour plonger dans la tête d’un de ces architectes du moyen-âge ! Alors est-ce que je peux me fier aux moins aux différentes mesures?

A/ Les mesures

Aujourd’hui si vous avez un meuble cassé à reconstruire il est très probable que si vous trouvez un meuble mesurant 1m87 de haut vous vous dites qu’il devait probablement mesurer 1m90. Oui parce que dans notre système décimal cela paraît tellement logique! Pourquoi s’arrêter à 1m87? Oui mais…

1/ Le système métrique.. C’est le pied!

On oublie : il n’existait pas.. Enfin… C’est plus complexe mais on va simplifier et rester sur une réalité architecturale en disant qu’on utilisait le pied. Oui au moyen-age c’était LA référence pour mesurer les longueurs et donc les superficies.
D’après ce plan Anglais de la cathédrale de Reims (voir image) on remarque sur la section centrale que 115 Pieds correspondent à 35mètres soit 1 pied = 0.305m et sur les sites de conversion en ligne on trouve plus précisément 0.3048m pour le pied Anglais. La chose surprenante et qui m’a induit en erreur au début c’est que j’ai vu que la cathédrale faisait exactement 100Pieds de large. Je me suis dit bingo un chiffre bien rond et je suis parti sur la base que tout a été calculé probablement sur des multiples de 0.305m.. Mais oui on est en France et malheureusement le pied du roi Anglais n’est pas le même que celui du roi Français = 0.3236m. qui dépend aussi de l’époque (pied du roi = 0.3248 après 1667) et de tout un tas de choses mais ce pied semblait un bon point de départ pour être une référence car c’est une mesure digitale (qui est physique, basé sur l’humain) et qui est donc utilisée depuis l’antiquité (et peut-être même avant)!
A ce pied s’ajoute d’autres mesures anciennes ‘fiables’ : ainsi 12 pouces = 1 pied et la toise = 6 pieds mais il existe aussi une multitude d’autres mesures comme la coudée, l’empan, etc qui sont utilisées depuis des millénaires. Essayons de retrouver les moyens de mesures et de tracés de l’époque qui pourrait aider à construire une cathédrale (tout ça en sachant que tout n’est pas tranché, qu’il y a de grands débats scientifiques, archéologiques sur tous ces sujets.. et que j’y ai passé qu’une semaine (enfin presque 2 vu que ma cervelle ne m’a pas laissé tranquille la nuit!).

Le décret du 1er août 1793 qui donne la naissance du mètre dont la longueur est établie comme « égale à la dix millionième partie du quart du méridien terrestre » 

B/ Les mathématiques pour calculer une cathédrale?

1) Le nombre d’or

Voilà un article très très long mais très intéressant qui résume un peu tout ce qui a été trouvé sur le net en tant que théorie, calcul etc
Attention les scientifiques, archéologues, etc seraient capables de sauter au plafond, de mourir d’un infarctus ou de s’auto étrangler en lisant ceci mais lisez le plus tard et avouez qu’il est intéressant de se questionner car si les faits sont réels, il faut toujours admettre que c’est bien leurs interprétations qui donnent la vérité propre à chacun (c’est beau ça lol). Voilà donc l’article :

2) La suite de Fibonacci

C’est la fameuse suite très simple qui est 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…. (1+1 = 2, 2+1 =3, 3+2=5, 5+3=8, etc). Cette suite est remarquable car elle approche toujours le nombre d’or (ou Phi)! En effet.. 3/2=1.5 puis 5/3= 1.666 puis 8/5=1.6 puis 13/8=1.625 puis 21/13=1.615.. 55/34=1.6176 etc
Rapporté à la canne on voit bien qu’on suit la même logique… La valeur suivante est l’addition des 2 premières.

3/ Comment mesurer?

1/ La quine ou la canne des bâtisseurs

Certains pensent que les architectes utilisaient un instrument très pratique : leur canne! L’argument est qu’un architecte peut être sur plusieurs chantiers et que la canne serait pratique à transporter..

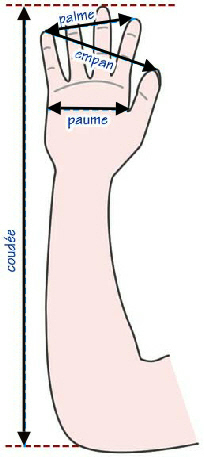
L’unité de base serait la ligne et la canne serait découpée en 555 lignes pour une longueur d’environ 1m25. La canne serait divisée en 5, correspondant au 5 valeurs étalon de l’époque qui sont écrites sur l’image. Choses remarquables :
1 coudée = 1 Pied + 1 Empan
1 pied = 1 Empan + 1 Palme, etc
On retrouve la notion de la suite de Fibonacci!

Plus fort certains disent qu’on utilisait le nombre d’or pour passer de l’un à l’autre :
La palme = la paume * 1,618 (7,64 * 1,618) = 12,36 cm
L’empan = la palme * 1.618 (12.36*1.618) = 20cm
Le pied = l’empan * 1,618 (20 * 1,618) = 32,36 cm
la coudée = le pied * 1,618 (32,36 * 1,618) = 52,36 cm
Et on constate que la coudée est toujours égale au pied + empan

Il y a cependant de vifs débats sur l’utilisation et même l’existence de cette quine d’autant plus que certains rapproche la coudée de cette canne à la coudée Égyptienne qui fait entre 52 et 54cm or on vient de voir que la coudée associée à la quine serait de 233lignes ou 32.36cm+20cm = 52.36cm… Mais bon si la quine n’existe pas… Passons…
Ce qui est sur c’est qu’on aime donner une grandeur divine aux cathédrales et que certains chiffres, coefficients se retrouvent partout dans le domaine des arts.. Mais était-ce voulu pour les cathédrales? A la renaissance on sait que le nombre d’or refait surface (L. de Vinci) mais au moyen-âge… Il va falloir continuer le lire pour savoir ce que j’en pense!

2/ La corde à 13 noeuds.

Mythe ou réalité certains rapprochent les pyramides d’Egypte aux cathédrales du moyen-age et même si cette corde n’a peut-être pas existé, les mêmes problèmes géométriques étaient à résoudre d’un côté comme de l’autre et ce procédé est tout aussi simple qu’efficace!

En effet l’idée de la corde est séduisante car elle reprend un fait établi en Egypte par le papyrys de Rhind qui montre que les égyptiens maitrisaient déjà parfaitement les problèmes géométriques pour la construction des pyramides mais aussi pour le calcul des aires et des volumes. Pour avoir un triangle rectangle il suffit d’avoir une base de 3 et une hauteur de 4 et que le dernier côté fasse 5! (https://fr.wikipedia.org/wiki/G%C3%A9om%C3%A9trie_dans_l%27%C3%89gypte_antique#Le_triangle_3-4-5)

Avec une corde a 13 noeuds (si on fait correspondre le premier et le dernier noeud) on a bien 3 + 4 + 5 et on peut donc vérifier rapidement un angle droit (https://fr.wikipedia.org/wiki/Corde_%C3%A0_n%C5%93uds

Je n’ai pas approfondi plus que ça et il y a aussi débat sur l’utilisation de ces cordes et comme visiblement on n’en a retrouvé aucune trace certains diront que c’est parce qu’elles se décomposent, d’autres qu’elles n’étaient pas utilisées et ce ne sont pas les écrits qui vont nous aider!

III /Conclusions personnelles

J’ai lu plein de choses, plein de théories et j’ai été émerveillé en me baladant aux 4 coins de l’univers mais revenons un peu sur terre! Je vais reprendre les 3 chapitres et vous donner mon avis. Je vous rappelle que je ne suis ni archéologue ni spécialiste en architecture ni mathématicien, etc mais cela ne m’empêche pas de penser (en plus c’est mon blog) 😀 alors..

1/ La règle des pieds?

Je suis désormais convaincu que les architectes (on peut parler d’architecte à partir du XII ième siècle) utilisaient forcément un étalon et des moyens simples de mesurer et de tracer comme 1 règle et 1 compas. Avec ces simples outils il est possible en effet de tout tracer. J’ai notamment survolé le livre « tracés des bâtisseurs » https://fr.calameo.com/read/0059767890b32fa4ecf3f) et je suis en train de vérifier certains tracés sur la cathédrale de Reims.

Maintenant est-ce que leur étalon correspondait à une valeur établie (comme 3 pieds ou comme la fameuse canne des bâtisseurs) et surtout est-ce que je peux me fier à cette valeur? Non… Il se trouve qu’à l’époque il y avait des centaines d’unités de mesure et on l’a vu : même le pied qui est censé être la référence varie (suivant les régions, les pays, les années, la perte de l’étalon, etc) donc à ce stade je ne peux pas me fier à une quelconque valeur de longueur.
Par contre il est tout à fait probable que chaque architecte utilise son étalon propre ce qui expliquerait pourquoi les mêmes rapports entre les dimensions reviennent fréquemment mais que les dimensions changent d’un monument à l’autre. Ainsi pour l’exemple 1 toise est toujours égale à 6 pieds donc on peut retrouver le rapport de 1/6ième dans plusieurs bâtiments mais comme 1 pied peut valoir 32 ou 30cm on trouvera rarement la même valeur en mètre… Les statistiques sur les mesures des portes de « Quentin Leplat » montrent ces rapports de mesure qui reviennent fréquemment. Principalement 33.3cm, 20cm et 52.3cm donc 1/3mètre, 20cm et 1 coudée royale Egyptienne..
Pourquoi retrouve-t-on principalement ces rapports? Je vais sûrement le découvrir en effectuant mes tracés…

2/ Les mathématiques Oui et Non…

Pas vraiment des calculateurs

Le moyen-age ne brillait pas par les sciences, cela redevient peut-être le cas aujourd’hui mais les architectes de l’époque n’avaient pas de calculatrice ni internet pour compenser… Alors j’ai essayé de me remettre dans le contexte de l’époque et j’ai copié/collé vite fait cette partie d’un article (désolé je ne sais plus où il était… trop de surf) qui vous y fera replonger également:

Le cahier de Villard de Honnecourt ignore superbement les mathématiques. Comme se plaisent à le dire les compagnons : « le trait pousse le nombre ». Nul besoin de béquille pour cet art qui considère le compas, la règle et l'équerre, comme les seuls outils permettant d'appréhender l'univers.
Les bâtisseurs médiévaux étaient issus d'une société découvrant à peine l'usage du zéro et additionnant laborieusement en chiffres romains...

Chose marrante il se trouve que Villard de Honnecourt (né en 1200+) était maître d’œuvre et qu’il a participé à la construction de la cathédrale de Reims! Cela vaut réellement le coup de s’intéresser à lui car c’est pratiquement la seule trace écrite sur la construction des cathédrales (faute à une tradition orale et au secret du compagnonnage?). Regardez ces pages et vous admettrez que même si le moyen-age n’était pas celui des maths ou de l’écrit ce carnet montre un sens aigu des proportions et des traits de génie :

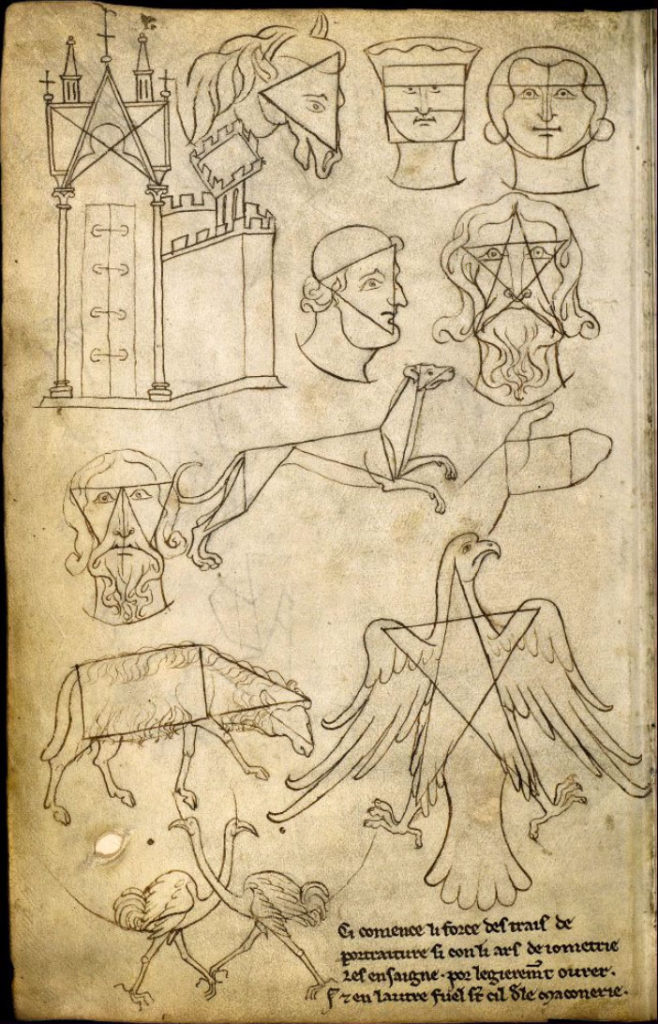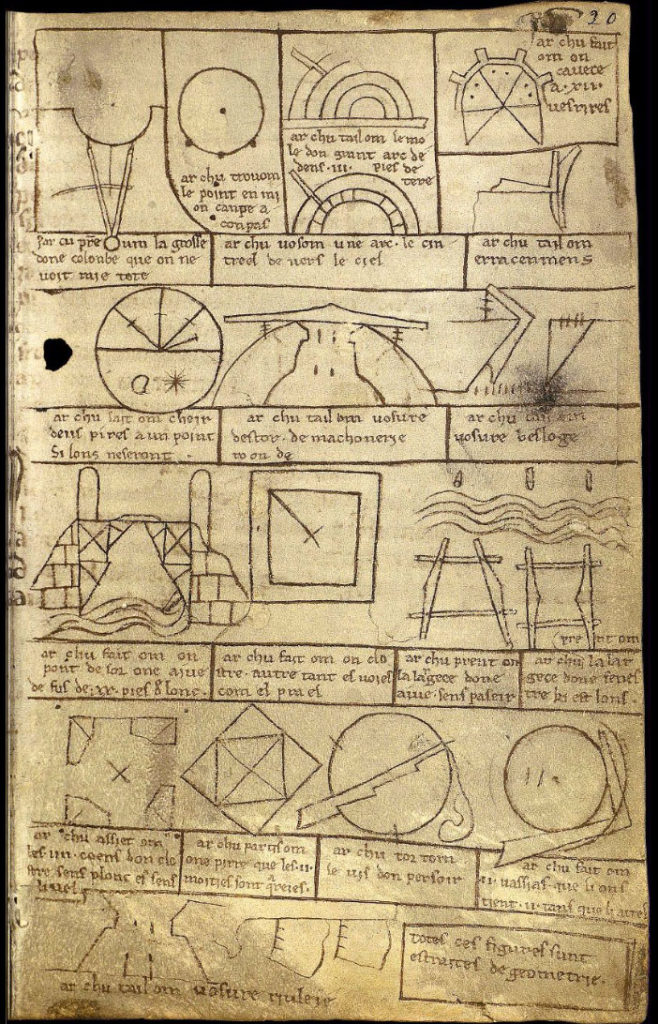On appréhende bien le fait maintenant que les rapports de distances devaient se cantonner à des fractions simples pour être efficaces ou que les tracés géométriques devaient pallier aux calculs.
La suite de Fibonacci a pourtant du sens car sans connaître le nombre d’or (Phi) précisément on voit bien qu’on peut s’en approcher simplement. De plus cet homme est né en 1175 à Pise et l’information circulait déjà…

Le nombre d’or comme étalon?

Est-ce que les architectes utilisaient consciemment les mathématiques et le nombre d’or? Je n’en sais rien mais je ne crois pas… Pourquoi? La chose intéressante c’est que ce nombre d’or est à l’origine de la divine proportion. Dans les « tracés des bâtisseurs » on s’aperçoit qu’ils pouvaient créer des triangles et des rectangles d’or sans passer par des mathématiques complexes : juste en traçant quelques arcs de cercles :

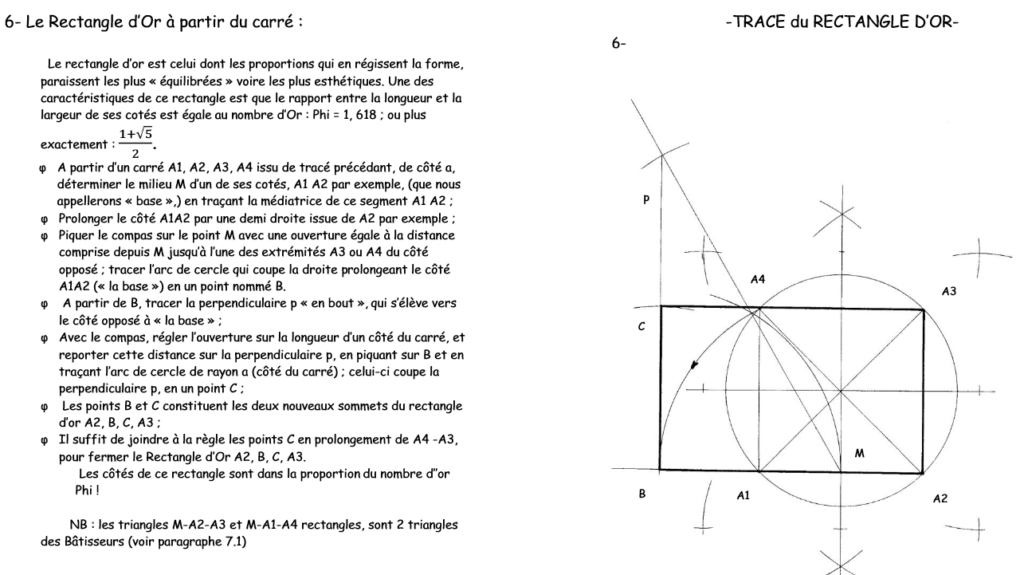
Il est donc tout à fait possible même s’ils ne connaissaient pas Pi, le nombre d’or, etc que leurs recherches les aient amené aux proportions parfaites!

Les Cathédrales… Egyptiennes?

Oui un super titre genre clic à.. Je vais être clair : non!
Mais je pense qu’il existe des valeurs universelles et pourquoi elles ne traverseraient pas les temps?

Ce qui est sur donc c’est que la coudée royale Egyptienne mesure entre 0.52 et 0,54m. Pourquoi? Contrairement à la canne des bâtisseurs, des exemplaires ont bien été retrouvés (https://fr.wikipedia.org/wiki/Coud%C3%A9e_royale_%C3%A9gyptienne). Elle servait bien à la construction rigoureuse de leurs monuments avec une précision remarquable.
Certains la mesurent même à exactement 0.5236mètres. Pourquoi? Ils aiment penser que PI/6= 0,523598 et que c’est grâce à cela qu’ils pouvaient calculer les volumes de leurs silos à grain, etc
Vous trouverez des experts frileux à cette idée mais étrangement l’idée personnellement me plait! Pourquoi? Car je suis romantique nan mais surtout parce que je doute qu’une telle dimension soit due au hasard or je n’ai rien trouvé qui montre que cette valeur soit une mesure digitale établie (comme la longueur d’un pied, etc). Personnellement quand je dois mesurer quelque chose de la taille d’un meuble spontanément sans instrument de mesure j’utilise l’écart entre mon pouce et le petit doigt… Vous pouvez vérifiez chez vous cela mesure +/- 20cm. Je ne suis pourtant pas Egyptien ni bâtisseur du moyen-age mais c’est une méthode si naturelle de faire qu’elle existe depuis des millénaires il se trouve que c’est l’Empan.

Pourquoi je prendrai comme valeur une coudée de 52.36cm? Oui effectivement c’est l’empan + la distance du poignet au coude mais comment vous pouvez mesurer naturellement quelque chose avec? Mesurez votre coudée comme le montre l’image… Vous obtenez 52cm? Non et d’ailleurs cette coudée beaucoup plus pratique dite petite coudée égyptienne existe et mesure 43 cm (je suis sûr que vous vous en approchez..). Bon j’avoue je n’ai pas cherché longtemps mais si on part du principe que ce n’est pas une valeur digitale pourquoi ne pourrait-on pas penser que cette valeur soit universelle comme le mètre basé sur une distance planétaire et qu’on puisse la retrouver par ‘hasard’ ailleurs?

Attention je ne dis pas qu’elle a été reprise consciemment dans l’architecture Française. La seule chose que je constate dans la figure qui démontre Pi/6 c’est qu’elle forme 6 triangles équilatéraux (3×60°) et je ne peux pas m’empêcher de rapprocher cette valeur avec le tracé de la première travée des cathédrales gothiques avec la voute de Barlong :

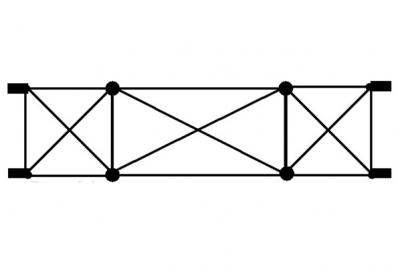
Oui il se trouve que cette voute se trouve aussi avec des triangles isocèles mais sur les cathédrales qui ont repris des fondations de type architecture Romane (carré). Et non il n’est pas fou de penser que des personnes même éloignées dans le temps puissent parvenir aux mêmes proportions en utilisant les mêmes outils…

Partons en vrille et soyons fous

Je ne suis pas un expert non plus en métrologie mais je me plais à penser que comme le mètre a été adopté en calculant un rapport à la circonférence de la terre et qu’on peut trouver une fraction de Pi dans la coudée Egyptienne (même un peu inexacte) un rapport peut exister :
a) On a vu le rapport à Pi or la terre tourne sur elle-même en un peu plus de 24h (elle fait bien une rotation de 360° et on parcourt 40000kms par jour). Pour rappel la terre n’est pas ronde et le mètre a été basé sur la distance au méridien. Si les Égyptiens s’étaient basés sur la rotation de la terre à l’équateur, la différence est peut-être due à la forme elliptique terrestre?
b) Comme beaucoup d’anciennes civilisations l’Égypte se basait en effet beaucoup sur l’observation du ciel et des mouvements des étoiles et les monuments d’Égypte ont tous un rapport particulier à la position des astres et en particulier du Soleil.
c) Comme base de calcul les Babyloniens utilisaient par exemple une base 12 (leurs phalanges sur 4 doigts), les Égyptiens ont dans leur système de mesure la palme (quatre doigts). La France a bien défini le mètre comme étant 1/4 de la distance du méridien de la terre donc 3/12. La terre fait le tour du soleil en 365 jours 1/4 jours donc 365 rotations de la terre qui ont été divisés en 12 mois… la notion de 1 toise = 6 Pieds = 12 Pouces… Enfin bref je m’égare mais je veux dire que les mêmes rapports reviennent et qu’on peut aussi relier la circonférence de la terre au temps qui passe. La base 60 de nos 60 secondes qui font 60min découlent des 360° de la terre.. Une base plus facile pour calculer le temps qui ont déjà fait que les Babyloniens ont découper l’année en 360jours. D’ailleurs pour définir le mètre on a pensé à utiliser des métronomes… Mètre.. Métronome…
Bref gros raccourci : la coudée Égyptienne = PI/6= 0,523598 et 1m/1.949 (hauteur d’une toise) = 0,513.. Sûrement un fantasme romantique (dont je vous ai fait un joli condensé argumenté lol)… Désolé!
Mon avis c’est qu’il est peu probable que les cathédrales aient été construites ou calculées sur un étalon ayant pour valeur la coudée Égyptienne. La réalité est je crois beaucoup plus pragmatique et encore basé sur l’utilisation du compas. Elle n’en demeure pas moins belle car basée sur des valeurs inaltérables et universelles!

3/ Les outils

Dans les possibilités certains auraient pu utiliser des outils pour accélérer leur travail : 1 triangle des bâtisseurs qui évite forcément d’avoir à retracer toujours le triangle d’Or, une corde à 13 nœuds pour tracer des carrés, des triangles rectangles etc mais il n’y a visiblement pas de preuves. L’idée de la canne des bâtisseurs est séduisante… A condition qu’il ne s’en serve pas trop pour marcher sinon c’est un coup à fausser toutes les mesures! Dans tous les cas le problème resterait pour moi le même : sans exactement le même outil à ma disposition savoir qu’ils en utilisaient ne me servirait à rien!

IV / Comment tracer la cathédrale de Reims

On dirait que je ne suis pas plus avancé et pourtant si!
Premièrement la cathédrale de Reims est d’architecture gothique dite classique et j’ai vu que ces cathédrales répondent bien à une architecture répétitive de formes mathématiques parfaites (même si ce n’était pas véritablement calculé, etc). Je peux donc modéliser chaque partie dans un ensemble cohérent et le dupliquer.

Grâce à Viollet-le-duc et son traité de l’architecture on sait que les cathédrales après le XIIième siècle répondent toutes à un plan de construction rigoureux donné par la position des piliers alors je sais par où commencer mon tracé : les entraxes des piliers! C’est censé me donner tout le plan d’élévation ou tout au moins les voutes de la nef principale. Chose remarquable : même si je n’ai pas la valeur de l’étalon ça ne m’empêche pas de commencer puisqu’il suffira de mettre un facteur d’échelle pour que tout se repositionne correctement!

Pour les hauteurs il y a aussi une relation géométrique due aux voutes, etc mais c’est plus complexe.. D’après mes premiers éléments il y a aussi un choix esthétique ou d’ordre pratique.. Par exemple la hauteur des piliers et du triforium définissent la hauteur des fenêtres hautes donc la façon d’éclairer l’intérieur de la cathédrale… A voir…

Autre chose dont je suis sûr. : pas la peine de sortir une calculatrice : je vais devoir tracer seulement des lignes et des cercles pour obtenir des carrés, des triangles isocèles ou équilatéraux!

Enfin même si le tracé original peut être rigoureux il faut aussi s’imaginer que les chantiers duraient longtemps, qu’il y a eu des contraintes géologiques, des améliorations de la conception de certaines parties grâce aux partages des expériences, etc Il ne faut pas perdre de vue que les cathédrales gothiques agrandissaient souvent des fondations d’origine romaines… Tout n’est pas forcément gothique.

V/ Conclusion…

Ma conclusion pour cet article c’est que..J’ai passé une semaine éprouvante et que des chiffres, des fractions, des tracés sont venus écourtés mes nuits 😀
Sérieusement? Même s’il y a beaucoup de fantasmes et de légendes autour du moyen-age les cathédrales resteront le chemin vers les divines proportions. Chemin temporel au cours des chantiers et des siècles et chemin spirituel car il fallait avoir une sacré foi pour construire de tels édifices en partant d’un compas.
Alors si certains veulent y voir la magie des mathématiques, des nombres d’or, etc On peut aussi sûrement les voir comme cela mais ce que je trouve encore plus beau c’est qu’au final on atteigne la perfection en partant de presque rien… C’est pour moi rassurant et un formidable message d’espoir dans une société où les mathématiques et la technologie semblent effacer tout le reste car au moins je sais que si tout disparait la beauté peut renaître simplement avec de la volonté et quelques cercles tracés.